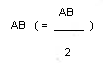Innenarchitektur . Goldener Schnitt Proportionen

Der Goldene Schnitt
Harmonie und Proportion in Kunst, Design, Innenarchitektur und Architektur

Die in der Natur herrschenden Verhältnisse des gleichseitigen Dreiecks, des Quadrates, des gleichseitigen Fünfecks und des Goldenen Schnittes sind den Menschen schon immer vertraut gewesen und von ihnen als "naturgemäß und wohlgefällig" und daher als schön empfunden worden. Die Kunst benutzte in allen Stilpochen, ganz besonders aber in der griechischen Antike, im Mittelalter und in der Renaissance die Formen, die die Natur ihr bot:

Die "Goldenen Proportionen" - Der Goldene Schnitt

Es ist im Menschen schon sehr früh die Erkenntnis gereift, dass der Harmonie ein verborgenes Gesetz zugrunde liegen muss. Die regelmäßige, wohlproportionierte Form der Kristalle, die Maßverhältnisse des menschlichen Körpers, die Maßverhältnisse im Bau von Tieren und Pflanzen, die Strukturgesetze der Musik, Malerei, Plastik und Baukunst unterliegen alle einem geheimnisvollen Zahlenverhältnis.

5 Methoden zur genauen Ermittlung des Goldenes Schnittes:

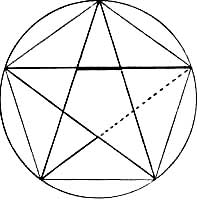
Das Pentagramm

Am regelmäßigen Fünfeck, dem Pentagramm, ergeben sich durch die Diagonalteilung große und kleine Abschnitte, wobei der kleine Teil zu einem größeren in demselben Verhältnis steht wie der größere Teil zur Summe von kleinen und großen Teilen.

Das Besondere am Pentagramm ist, dass sich hier nicht der angenäherte, sondern der mathematisch genaue Goldene Schnitt ergibt.

 

Die Pythagoreer waren die ersten, die den genauen Begriff der Harmonie und ihrer Messbarkeit entdeckten. Schon im 6. Jahrhundert v. Chr. haben sie in der griechischen Philosophenschule den Versuch unternommen, das Gesetz der Harmonie zu er-messen.

Nachdem ihre Experimente im Bereich der Musik zunächst zum Dreiklang aus Terz, Quinte und Oktave, also der mathematischen Konstante 3:5:8 geführt hatten, entdeckten sie später  am regelmäßigen Fünfeck, also am Pentagramm ein harmonisches Verhältnis zweier Strecken zueinander als Goldenen Schnitt. Dieses "göttliche Verhaltnis" der Harmonie hat die griechische Kunst und später die Renaissance stark beeinflusst

Baumeister des Altertums, der Romanik und Gotik und auch die Baumeister späterer Stilepochen bauten nach diesem als Geheimnis für Eingeweihte streng gehüteten Gesetz von "Maß und Zahl" viele Bauwerke, die noch heute als zeitlos (keiner Moderichtung unterworfen) angesehen werden.

Die Bezeichnung Goldener Schnitt stammt aus dem Mittelalter, einer Zeit, in der dieser Proportion offensichtlich große Bedeutung gegeben wurde. (Pacioli, 15./16. Jh., gab ihr bereits den Namen proportione divina = göttliche Proportion.)

Albrecht Dürer hat sich in seiner "Proportionslehre" (1528) mit den "Schlüsselfiguren": dem Dreieck, dem Quadrat, dem Fünfeck und ihren Maßverhältnissen auseinandergesetzt.

Der französische Bildhauer Rodin schrieb über die Beziehung der Natur zur Kunst: Zitat: "...und die Blumen haben die Kathedralen geschaffen... Die Kathedrale ist im Ebenbild der lebenden Körper erbaut. Ihre Proportion, ihre Gleichgewichtsbeziehungen entsprechen genau der Ordnung in der Natur." (Zitat Ende).

1. Die Ermittlung des Goldenen Schnittes

Das Verhältnis des Goldenen Schnittes beruht auf einer feststehenden Regel von größter Genauigkeit. Die Formel dafür heißt:

Die kürzere Strecke verhält sich zur längeren
wie die längere zur ganzen ungeteilten Strecke.

Wenn man also eine gegebene Linie so in zwei ungleiche Teile teilt, dass sich der entstandene kleinere Teil zum größeren so verhält wie der größere zur ganzen Linie, ist diese nach dem Goldenen Schnitt geteilt:

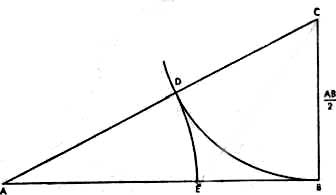
Man errichtet am Endpunkt B der Strecke AB eine Senkrechte, auf der man von B aus die Hälfte

abträgt. Um C schlägt man mit CB einen Kreis.

Verbindet man C mit A, so schneidet diese Linie den Kreis im Punkt D. Schlägt man um Punkt A mit AD einen Kreis, so schneidet dieser die Strecke AB in Punkt E und teilt sie nach dem Goldenen Schnitt.

Die Länge EB verhält sich nun zu AE wie AE zur ganzen Strecke AB.

2. Eine weitere Methode zur Ermittlung des Goldenen Schnittes

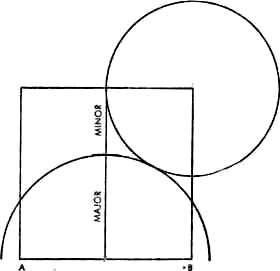
Diese Methode zur Ermittlung des Goldenen Schnittes arbeitet mit dem Quadrat und zwei Kreisen:

Man erstellt auf der nach dem Goldenen Schnitt zu teilenden Grundlinie AB ein Quadrat, das senkrecht in der Mitte geteilt wird.

Dann schlägt man um eine obere Ecke einen Kreis mit der halben Quadratseite als Radius.

Schlägt man nun um die Mitte der Grundlinie einen weiteren Kreis, so groß, daß dieser den oberen Kreis berührt, so wird die senkrechte Mittellinie dort, wo der zweite Kreis diese schneidet, nach dem Goldenen Schnitt geteilt.

3. Die Goldene Reihe

Den Goldenen Schnitt kann man auch als Goldene Reihe wie folgt ermitteln:

Die in C nach dem Goldenen Schnitt geteilte Gerade AB kann man weiter nach diesem Verhältnis unterteilen, indem man die Länge CB von A aus bis D abträgt. Dann ist auch AD:DB=DB:AB, hat also jede begrenzte Gerade zwei "harmonische" Teilungspunkte.

Der Zwischenraum zwischen den beiden gefundenen bzw. ermittelten Punkten, die Strecke DC, steht dann ebenso im Goldenen Verhältnis zu AD und CB, so dass nun die Minoren AD und CB der Strecke AB die Majoren zu DC darstellen.

Verlängert man die Strecke AB über A hinaus um die gleiche Strecke bis D, so bilden die dadurch entstandenen drei Strecken eine sogenannte "Goldene Reihe".

Die Vergrößerung kann man ebenso wie die Verkleinerung bis ins Unendliche weiterführen. Die auf diese Art ermittelten Strecken stehen dann im Goldenen Verhältnis oder im sogenannten "Goldenen  Zirkel".

Bei dieser Ermittlungsweise der Goldenen Reihe ist es zum Beispiel möglich, statt der Proportion 3:5 oder 5:8 auch andere Proportionen wie z.B. 3:8 zu ermitteln.

Dies kann wichtig werden, wenn eine bestimmte gestalterische Absicht oder durch die durch den Zweck eines Bauwerkes vorgegebenen Grundmaße mit den "normalen Proportionen des Goldenen Schnitts" nicht erreicht werden können. Das kann z.B. bei der Gestaltung und Konstruktion von Möbeln oder von Bauwerken durchaus der Fall sein.

4. Den Goldenen Schnitt rechnerisch ermitteln

Will man das Verhältnis des goldenen Schnittes in Zahlen ausdrücken, muss man Zahlen wählen, die dieses Verhältnis annähernd genau wiedergeben, also nur ganze Zahlen, die nach einer bestimmten Formel entstehen.

Die Zahlenreihe, die annährend dem Goldenen Schnitt entspricht, ist die sogenannte Lame´sche Reihe:

1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 usw.

Diese Zahlen erhält man einfach, indem man die vorangegangene Zahl zum Ergebnis dazuzählt:

1+1=2 +1=3 +2=5 +3=8 +5=13+8=21 +13=34 +21=55 +34=89 +55=144 +89=233 +144= 377 usw.

Diese Zahlen drücken das Verhältnis zwar nicht ganz genau aus, dafür sind sie leicht zu ermitteln.

5. Konstruktion des Goldenen Schnittes ohne Zirkel

Hat man keinen Zirkel zur Hand, kann man noch die folgende einfache Methode zur Ermittlung des Goldenes Schnittes anwenden:

Man teilt die betreffende Strecke in acht gleichgroße Teile und nimmt dann bei drei und fünf die harmonischen Teilungspunkte an.

Beispiel:
Die angenommene Strecke AB ist 24 cm lang, man rechnet wie folgt:

24 : 8	=  3
3 x 5	=  15	= Teilstrecke Major
3 x 3	=  9	= Teilstrecke Minor

6. Üblich ist auch die Angabe des goldenes Schnittes im Zahlenverhältnis:

1 : 1,618

Der goldene Schnitt in der praktischen Anwendung

Wenn es auch heutzutage nicht mehr so häufig geschieht wie in früheren Epochen - die Proportionslehre und den goldenen Schnitt kann man heute genauso anwenden wie die alten Meister es taten - in der Architektur, Innenarchitektur und im Design jeder Art, bei Bauwerken genauso wie bei Möbeln oder in der Gartengestaltung...

Durch das Befolgen der altehrwürdigen Proportionslehre erhalten eine Eingangstür, ein Fenster, eine Fassadengestaltung, eine Raumaufteilung oder ein modernes Designermöbel einen harmonischen Anblick, das besondere Etwas, das den meisten Menschen nicht offensichtlich auffällt, aber besonders gut gefällt.

 

Falls Sie momentan mehr an der praktischen Anwendung von Stilen und Stilkunde-Kenntnissen interessiert sind, weil Sie ein eigenes Projekt gestalten möchten, falls Sie kompetente Hilfe beim Bauen, Einrichten und Ausstatten brauchen, dann finden Sie hier
persönliche Beratung

 

über die Autorin

 

nach oben